Trong khuôn khổ bài viết này, mình sẽ viết về vấn đề Danh pháp cis-trans của hệ nối đôi. Còn danh pháp cis-trans cho hệ vòng no các bạn xem bài viết sau:
Trong đó \(a \ne b\).
Khoảng cách giữa các nguyên tử trong phân tử (X), (Y) khác nhau rất lớn, do đó về phương diện hình học thì (X), (Y) có hình dạng, kích thước phân tử khác nhau nên đại lượng Entalpi tự do tạo thành cũng khác nhau, các hằng số vật lý, các đặc trưng về phổ và cuối cùng là tính chất hóa học cũng khác nhau rõ rệt. Bởi vậy đó cũng là một nguyên nhân X và Y là 2 đồng phân của nhau.
Hệ thống danh pháp cis-trans áp dụng tốt cho các đồng phân hình học có dạng \(abC = Cba\) và \(abC = Cac\) (viết gọn là \(axC = ay\)) , a cùng phía so với mặt phẳng cố định là dạng cis-, ngược lại khác phía là dạng trans-.
-Sử dụng mô hình \(axC = ay\) theo hình vẽ sau để xác định đồng phân cis-trans: (Sử dụng bằng cách so sánh và đối chiếu)
-Nếu mỗi carbon có 2 nhóm thế khác nhau \(R \ne R'\) thì số đồng phân hình học là \({2^n}\).
Nếu \(R = R'\) thì số đồng phân hình học giảm vì đồng phân cis-trans tương đương với đồng phân trans-cis.
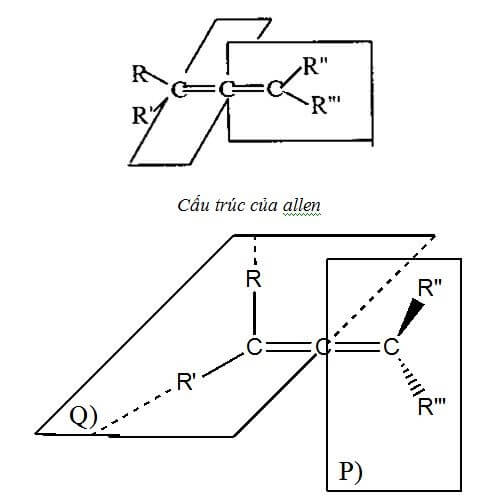
Khoảng cách giữa R’’ và 2 nhóm thế trên mặt phẳng Q là tương đương với khoảng cách của nhóm thế R’’’ và 2 nhóm thế trên mặt phẳng Q.
\({d_{R'' - R}} = {d_{R'' - R'}}\) và \({d_{R''' - R}} = {d_{R''' - R'}}\)
Với trường hợp này ta thấy rõ, rõ ràng hệ allen là một hệ cứng nhắc, tuy nhiên không thể xuất hiện đồng phân hình học vì một lý do, khoảng cách của một nhóm thế trên 1 mặt phẳng so với 2 nhóm thế khác trên mặt phẳng còn lại là giống nhau. Tức R ở vị trí của R’ cũng giống như nó đang ở vị trí hiện tại của nó vậy, đều cùng là một chất.
\( \Rightarrow \) Mở rộng, các chất có số liên kết đôi chẵn liền liên tiếp sẽ không có đồng phân hình học. (ở đây là đồng phân cis-trans).
* Hợp chất có số liên kết đôi liền liên tiếp là số lẻ như cumulen thì có đồng phân hình học vì các nhóm thế nằm trong cùng một mặt phẳng.
Tựa lời:
Bài viết có thể còn thiếu sót, mình hy vọng sẽ đóng góp ý kiến để nó hoàn thiện hơn. Các bạn vui lòng comment phía dưới để đóng góp ý kiến. Nếu các bạn copy, vui lòng để lại nguồn vì công sức bỏ ra là không ít đâu nhá.
Đồng phân hình học ở các hệ vòng
Xem tất cả bài viết về chuyên đề: Series chuyên đề đồng phân hình học
Hệ danh pháp cis-trans (Đồng phân cis-trans)
Các đồng phân cis-trans cho nối đôi có mô hình chung như sau: \(abC = Cba\)
Khoảng cách giữa các nguyên tử trong phân tử (X), (Y) khác nhau rất lớn, do đó về phương diện hình học thì (X), (Y) có hình dạng, kích thước phân tử khác nhau nên đại lượng Entalpi tự do tạo thành cũng khác nhau, các hằng số vật lý, các đặc trưng về phổ và cuối cùng là tính chất hóa học cũng khác nhau rõ rệt. Bởi vậy đó cũng là một nguyên nhân X và Y là 2 đồng phân của nhau.
Table of contents:
- Đồng phân hình học Hệ một nối đôi
- Đồng phân cis-trans hệ đa nối đôi
- Đồng phân hình học của hệ nhiều nối đôi liên tiếp
- Đồng phân hình học trong hệ thống ethylen phức tạp
Nội dung
Danh pháp cis-trans của nối đôi
∎Đồng phân hình học Hệ một nối đôi
-Công thức chung:Hệ thống danh pháp cis-trans áp dụng tốt cho các đồng phân hình học có dạng \(abC = Cba\) và \(abC = Cac\) (viết gọn là \(axC = ay\)) , a cùng phía so với mặt phẳng cố định là dạng cis-, ngược lại khác phía là dạng trans-.
-Sử dụng mô hình \(axC = ay\) theo hình vẽ sau để xác định đồng phân cis-trans: (Sử dụng bằng cách so sánh và đối chiếu)
Ví dụ:
-Mặt phẳng cố định là mặt phẳng cứng π: (minh họa bởi các hình vẽ sau)
mặt phẳng π (Q) vuông góc với mặt phẳng liên kết (P).
Chú thích:
- Đồng phân cis-trans là đồng phân đia (đi-a) của nhau.
Câu hỏi đặt ra: Đồng phân đia là gì?
∎ Đồng phân cis-trans hệ đa nối đôi
-Đối với hệ nhiều nối đôi quy tắc cis-trans tương tự hệ một nối đôi khi ta xét 1 nối đôi cụ thể: Ngày nay để thuận tiện cho việc gọi tên, việc sử dụng hệ danh pháp Z-E thuận tiện hơn cho việc gọi tên các đồng phân này.-Nếu mỗi carbon có 2 nhóm thế khác nhau \(R \ne R'\) thì số đồng phân hình học là \({2^n}\).
Xem thêm: Cách tính nhanh số lượng đồng phân hình học và phương pháp tính
∎ Đồng phân hình học của hệ nhiều nối đôi liên tiếp
* Hợp chất loại allen không có đồng phân hình học: Vì các nhóm thế nằm trong 2 mặt phẳng khác nhau.\({d_{R'' - R}} = {d_{R'' - R'}}\) và \({d_{R''' - R}} = {d_{R''' - R'}}\)
Với trường hợp này ta thấy rõ, rõ ràng hệ allen là một hệ cứng nhắc, tuy nhiên không thể xuất hiện đồng phân hình học vì một lý do, khoảng cách của một nhóm thế trên 1 mặt phẳng so với 2 nhóm thế khác trên mặt phẳng còn lại là giống nhau. Tức R ở vị trí của R’ cũng giống như nó đang ở vị trí hiện tại của nó vậy, đều cùng là một chất.
\( \Rightarrow \) Mở rộng, các chất có số liên kết đôi chẵn liền liên tiếp sẽ không có đồng phân hình học. (ở đây là đồng phân cis-trans).
* Hợp chất có số liên kết đôi liền liên tiếp là số lẻ như cumulen thì có đồng phân hình học vì các nhóm thế nằm trong cùng một mặt phẳng.
Cấu trúc của các cumulen
Thực tế người ta đã tách được 2 đồng phân hình học của loại hợp chất có cấu trúc như cumulen [3].
\( \Rightarrow \) Mở rộng, các chất có số liên kết đôi lẻ liền liên tiếp thì có đồng phân hình học.
Cách gọi tên cis-trans tương tự như hệ một nối đôi:
∎ Đồng phân hình học trong hệ thống ethylen phức tạp
Một hệ thống vòng tạo nên 1 hệ cứng nhắc trên một mặt phẳng.
Tài liệu Tham khảo:
3. PGS.TS Thái Doãn Tĩnh (2008), Cơ chế và phản ứng hóa học hữu cơ tập 1, Nhà xuất bản khoa học và kỹ thuật, pp. 148-244.
4. Võ Thị Thu Hằng (2002), Hóa học lập thể, TRƯỜNG ĐẠI HỌC SƯ PHẠM TP. HỒ CHÍ MINH ( KHOA HÓA ), TP Hồ chí minh, pp. 6-7; 46-49.
Tựa lời:
Bài viết có thể còn thiếu sót, mình hy vọng sẽ đóng góp ý kiến để nó hoàn thiện hơn. Các bạn vui lòng comment phía dưới để đóng góp ý kiến. Nếu các bạn copy, vui lòng để lại nguồn vì công sức bỏ ra là không ít đâu nhá.
Đăng nhận xét